Hierbei ist nicht nur die Kenntnis der Dauerleistung des Widerstandes notwendig, sondern auch die der Pulsbelastbarkeit. Durch eine Kombination aus theoretischen Grundlagen und Finite-Elemente-Simulationen der elektrischen und thermischen Belastung dieser Widerstände lässt sich die Pulsbelastbarkeit drahtgewickelter Leistungswiderstände über einen weiten Pulsdauerbereich sehr gut bestimmen. Die Ergebnisse können generalisiert und Kundenspezifikationen hinsichtlich der Einsetzbarkeit schnell bewertet werden.
Widerstand ermöglicht Pulsbelastbarkeit
Üblicherweise sind drahtgewickelte Leistungswiderstände bezüglich ihrer Dauerleistung spezifiziert. Bei der Verwendung von Draht als Widerstandselement kann dieses, aufgrund der relativ hohen Wärmekapazität des Drahtes, relativ viel Energie aufnehmen, wobei der Temperaturanstieg moderat ausfällt. Daher eignen sich drahtgewickelte Leistungswiderstände für Applikationen mit Pulsbelastungen sehr gut.
Durch den immer häufigeren Einsatz, beispielsweise in Frequenzumrichtern, erfährt auch die Spezifikation der Aufnahmefähigkeit von Pulsbelastungen größere Wichtigkeit. Dies geschieht oft exemplarisch durch Angabe der maximal zulässigen Leistung für einen Puls mit einer gewissen Dauer oder der damit verbundenen Pulsenergie.
Hin und wieder werden auch die maximal zulässigen Energien oder Leistungen für Pulse mit unterschiedlichen Dauern angegeben. Wird der Widerstand nun einer Pulsbelastung ausgesetzt, deren Dauer im Bereich nicht-adiabatischer Randbedingungen liegt und schwierig mit den im Datenblatt angegebenen Werten für Kurzzeitimpulse vergleichbar ist, so ist die Berechnung der maximal zulässigen Pulsbelastbarkeit für diesen Fall keinesfalls trivial. Möglich wird sie durch eine Kombination aus theoretischen Grundlagen und Finite-Elemente-Simulationen der elektrischen und folglich thermischen Belastung des Widerstands.
E-Mobility benötigt Pulsbelastbarkeit
Im Bereich E-Mobility ist die Begrenzung des Lade- und Entladestroms von Kondensatoren eine typische Anwendung für drahtgewickelten Leistungswiderstände, da hierbei hohe Pulsbelastungen für die Widerstände auftreten. Es werden gerne mehrere kleine drahtgewickelten Leistungswiderstände auf ein PCB gelötet, um die Herstellung einfach zu gestalten. Für diese Applikation liegt bei Vishay der Fokus auf der AC-AT-Serie, die als erste ihrer Art nach AEC-Q200 Automotive qualifiziert wurde.
Pulsbelastung erzeugt Wärme
Um den thermischen Effekt eines elektrischen Pulses auf einen Widerstand bewerten zu können, muss man das Abkühlen des Widerstands betrachten. Effektiv geschieht das beispielsweise durch die Annahme, dass Newtonsche Abkühlung vorliegt, das heißt dass die zeitliche Abnahme der Temperatur proportional der Temperaturdifferenz zwischen heißem Widerstand und dessen kühlerer Umgebung ist, und dass die Temperatur der Umgebung konstant bleibt. Übertragen auf das Widerstandselement, also den heißen Draht, besteht dessen Umgebung (in unserem Fall der AC-Serie) aus Zement. Die folgenden Überlegungen können aber auch auf glasierte oder sandgefüllte drahtgewickelte Leistungswiderstände übertragen werden.
Unterschätzte Pulsbelastbarkeit
Die Annahme Newtonsche Abkühlung und damit der Proportionalität von zeitlicher Änderung der Temperatur und maximaler Temperatur des Drahts oder besser des Widerstands, führt dazu, dass die Temperaturen von Draht und gesamtem Widerstand durch Exponentialfunktionen beschrieben werden können. Die Grenzen der Pulsbelastbarkeit sind für einen AC05-Widerstand mit 47 Ω und dessen Widerstandsdrahts in Abbildung 1 in blau beziehungsweise rot gezeigt.
Die maximale Pulsbelastbarkeit des gesamten Widerstandes wird in der Regel durch eine einfache Kombination beider Kurven dargestellt. Eine Möglichkeit ist eine Exponentialfunktion vom Typ der Newtonschen Abkühlung, Kombination 1 in Abbildung 1, die jedoch weit unterhalb der üblichen Überlastbarkeit von zehnfacher Nennleistung für 5 Sekunden liegt, und damit die Pulsbelastbarkeit in diesem Bereich ganz klar unterschätzt.
Überschätzte Pulsbelastbarkeit
Eine zweite Möglichkeit, Kombination 2 in Abbildung 1, überschätzt jedoch die Pulsbelastbarkeit im Bereich des gezeigten Knicks, bei etwa 0,05 s, da die Erwärmung des Widerstandskörpers bei der Berechnung für den Draht nicht berücksichtigt wird.
Simulation für beliebige Pulsdauer
Finite-Elemente (FE)-Simulationen der Wärmeströmung und der Temperaturverteilung im AC05 Widerstand führen bei einer pulsierenden Wärmequelle im Draht, aufgrund einer elektrischen Pulsbelastung, nicht nur zur Erwärmung des Drahts und darauf folgender Abkühlung, sondern natürlich auch zur entsprechenden Erwärmung des gesamten Widerstands mit einer gewissen Verzögerung. In der FE-Simulation spielt die Dauer der Pulsbelastung keine Rolle, sofern die Randbedingungen richtig gewählt sind. Somit lassen sich die Temperaturen vom Draht und auch des Widerstandes für beliebige Pulsdauern, von adiabatisch aus Sicht des Drahts (ms-Bereich) bis quasi zu Dauerlast des gesamten Widerstands (100-s-Bereich), simulieren. Durch die Vorgabe maximal zulässiger Temperaturen im Draht lässt sich so auch die maximal zulässige elektrische Pulsbelastung ermitteln.
Generalisierung durch Skalierung
Die durch einige FE-Simulationen erhaltenen Ergebnisse lassen sich durch Skalierung mit der charakteristischen Zeit für thermische Diffusion des Drahts bezüglich der Pulsdauer generalisieren. Daraus kann ein Korrekturfaktor in die Exponentialfunktion eingebracht werden, die die Temperatur gemäß der Newtonschen Abkühlung beschreibt.
Kontinuierliche Belastbarkeit des Widerstands
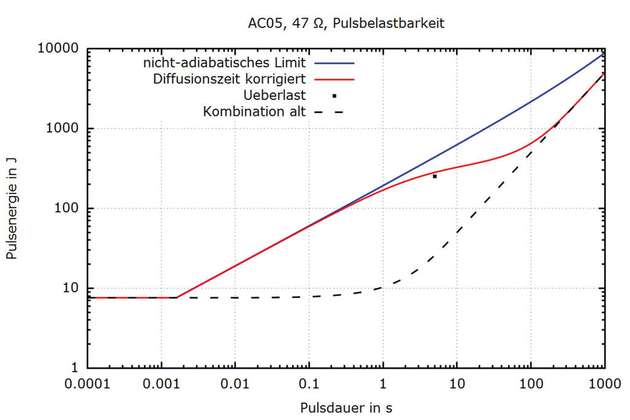
Mit den genannten Korrekturfaktoren lässt sich die maximal zulässige Pulsbelastung für nicht-adiabatische Randbedingungen aus Sicht des Drahts berechnen (Abbildung 2, nicht-adiabatisches Limit). Diese konvergiert jedoch für lange Pulsdauern nicht gegen die Pulsbelastbarkeit des gesamten Widerstands. Benutzt man aber für relativ lange Pulsdauern zur Skalierung die charakteristische Zeit für thermische Diffusion des gesamten Widerstands, so konvergiert die Grenzkurve der Pulsbelastbarkeit unter nicht-adiabatischen Randbedingungen gegen die Grenzkurve für die kontinuierliche Belastbarkeit des Widerstands.
Übertragung auf andere Verfahren möglich
Die Ergebnisse der FE-Simulation der thermischen Eigenschaften eines bestimmten Widerstands, hier des AC05 mit
47 Ω, lassen sich durch geeignete Skalierung generalisieren und daher ohne weitere FE-Simulationen nicht nur auf alle Widerstandswerte (Drahtkonfigurationen) des AC05, sondern auf alle AC-Typen übertragen, da sich diese in ihrer Bauart sehr ähnlich sind.
Das Verfahren ist sogar auf alle anderen ähnlichen drahtgewickelten Widerstände, wie beispielsweise die G200-Serie, ohne zusätzliche FE-Simulationen übertragbar und daher extrem effizient. Für den Anwender hat das den Vorteil, dass Fragen nach der Pulsbelastbarkeit kompetent und sehr schnell beantwortet werden können.












.jpg)


