Eingangsfilter sind wichtige Bestandteile moderner Leistungselektronik, welche unerwünschte Emissionen verringern oder bestenfalls komplett eliminieren. Folglich benötigen auch Leistungsmodule oft einen Eingangsfilter, um die EMV-Prüfung zu bestehen. Neue Power-Module, wie die MagI3C-Serie von Würth Elektronik, sind optimiert auf eine geringe leitungsgebundene und abgestrahlte Störaussendung. Ihre Restwelligkeit weist in der Regel einen vernachlässigbar kleinen Wert auf, sodass in den meisten Anwendungsfällen auf einen Ausgangsfilter verzichtet werden kann. Weil der Eingangsstrom beim Abwärtswandler pulsierend ist, können in der Applikation Funkstörungen (Gegentaktstörungen) entstehen. In Abhängigkeit der Applikation entscheidet der Hardwareentwickler, ob ein Eingangsfilter direkt vor dem Power-Module benötigt wird oder an einer anderen Stelle der Schaltung zum Einsatz kommt. Im Folgenden wird der Entwurf von Eingangsfiltern für die MagI3C-Power-Module von Würth Elektronik und die hierfür verwendeten Messverfahren vorgestellt.
Auftreten von Funkstörspannungen
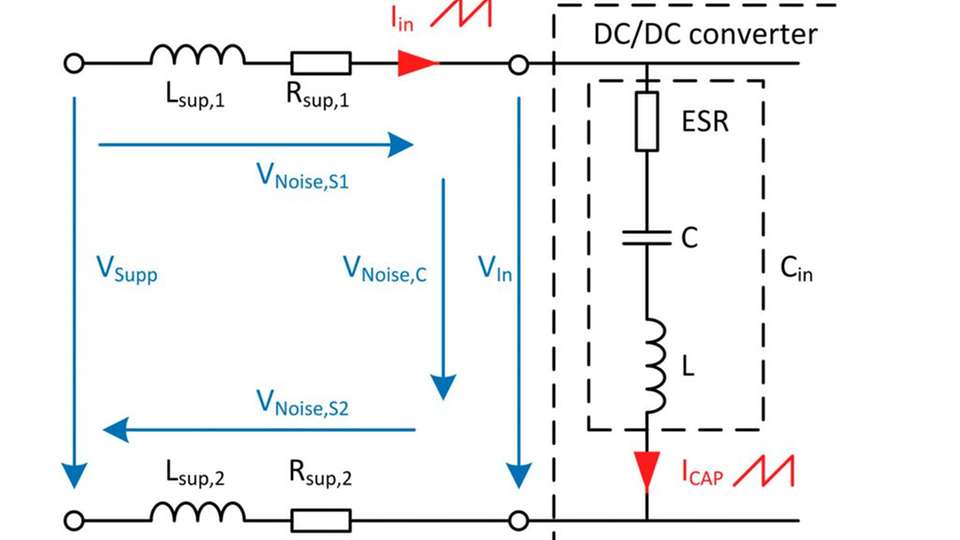
In den Zuleitungen eines Schaltreglers treten unvermeidliche Gegentaktstörungen (Differential Mode Noise) auf. Allgemein ausgedrückt, sind das Störsignale in einem System mit symmetrischem Stromfluss hin und zurück zur Quelle (Source). Im Eingangskreis fließt mit der Taktfrequenz des Power-Moduls ein dem Nutzstrom überlagerter Wechselstrom-
anteil. Dieser ähnelt im Abbild dem Strom, der durch die Speicherinduktivität des Power-Moduls fließt. Der Eingangsstrom fließt in den Eingangskondensator Cin.
Reale Kondensatoren verfügen über einen resistiven Anteil, den ESR (Equivalent Series Resistance, Serienwiderstand) und einen induktiven Anteil, den ESL (Equivalent Series
Inductivity L, Serieninduktivität). Der Wechselstromanteil führt über den ESR des Eingangskondensators und den Impedanzen der Zuleitungen des Power Moduls zu einem unerwünschten Spannungsabfall. In dieser Form liegt die Funkstörspannung als Gegentaktsignal (Gegentaktstörung) vor. Die Amplitude der Störspannung, welche am Eingangskondensator entsteht, hängt maßgebend vom ESR des verwendeten Kondensators ab.
Elektrolytkondensatoren verfügen über einen relativ hohen ESR, dessen Wert einige Milliohm bis einige Ohm aufweisen kann. Folglich kann die Störspannung wenige Millivolt bis einige Volt betragen. Keramikkondensatoren weisen dagegen einen sehr kleinen ESR von wenigen Milliohm auf und führen zu einer Störspannung von wenigen Millivolt. Zusätzlich beeinflusst auch das Leiterplattenlayout des Power-Moduls die Störspannung.
Berechnung eines LC-Eingangsfilters
Zum Reduzieren der Gegentaktstörungen (Funkspannungsstörungen) ist mindestens ein einfacher LC-Filter am Eingang des Wandlers erforderlich, der den Wechselstromanteil in den Zuleitungen auf ein Minimum reduzieren soll. Solch ein Eingangsfilter ermöglicht in hochohmigen Systemen theoretisch eine Spannungsdämpfung von 40 Dezibel pro Dekade im Sperrbereich. In der Praxis wird eine geringere Dämpfung erreicht, weil die Abschlussimpedanzen eher niederohmiger Natur sind und außerdem die Bauteile selbst Verluste aufweisen.
Zur Dimensionierung des LC-Filters wird eine Eckfrequenz fC gewählt, welche unter der Schaltfrequenz fsw des Power-Moduls liegt. Ist der Faktor ein Zehntel, wird bei der Schaltfrequenz, bei der die höchste Spektralamplitude auftritt, theoretisch eine Einfügedämpfung von 40 dB erreicht: fC = fSW/10. Die Eckfrequenz eines LC-Filters ist allgemein: fC =1/(2π * √(Lf * Cf).
Zur Berechnung des Filters wird beispielsweise eine Induktivität von 10 Mikrohenry gewählt und die vorherige Gleichung nach Cf umgestellt: Cf = 1/((2π * 0,1 * fSW)2 * Lf). Bei der Anordnung der Filterbauteile kann der Filterkondensator auf der Spannungsquellenseite oder auf der Seite des Power-
Modul-Eingangs platziert sein. Entscheidend für die Dämpfung, des aus der Spannungsquelle gezogenen pulsierenden Stroms, ist die Induktivität der Filterspule.
Dämpfung des Eingangsfilters
Bei einer zu hohen Güte der Filterresonanz können bei Eingangsspannungsänderungen, die ausgeregelt werden müssen, Oszillationen auftreten. Als Stabilitätskriterium gilt, dass die Ausgangsimpedanz des Eingangsfilters Zout,filter in einem weiten Frequenzbereich unter der Eingangsimpedanz des Power-Moduls Zin,converter liegen muss: |Zout,filter| < |Zin,converter|. Zusätzlich soll die Eingangsfilter-Eckfrequenz fc sehr weit unter der Durchtrittsfrequenz fco (crossover frequency) des Power-Moduls liegen: fc,filter << fco,converter. Hierzu wird ein Dämpfungszweig parallel zum Power-Modul-Eingang geschaltet. Das Dämpfungsglied reduziert die Güte des Eingangsfilters und folgend seine Ausgangsimpedanz bei der Resonanzfrequenz. Anhand der folgenden Gleichung kann der Dämpfungswiderstand Rd für eine Filtergüte von Qf = 1 berechnet werden: Rd =√(Lf/Cf). Als Praxiswert der Kapazität des Dämpfungskondensators Cd hat sich ein Wert etabliert, der dem Fünf- bis Zehnfachen der Filterkondensatorkapazität entspricht: (5 * Cf) < Cd < (10 * Cf).
Um den Filter zu dämpfen, kann alternativ ein einzelner Elektrolytkondensator gewählt werden, der anstelle eines Dämpfungsglieds parallel zum Filterausgang geschaltet wird. In der Regel hat der ESR des Elektrolytkondensators einen ausreichenden Wert, um den Filter zu dämpfen.
Auswahl der LC-Filter-Bauelemente
Sowohl Kondensatoren als auch Spulen, weisen in der Realität ein kapazitives und induktives Verhalten auf. Filterspulen haben bei ihrer Eisenresonanzfrequenz die größte Filterwirkung. Die Eigenresonanzfrequenz ist bei Spulen stark abhängig von der Induktivität und der kapazitiven Kopplung zwischen den Wicklungen. Beim Kondensator ist die Eigenresonanzfrequenz stark von der Kapazität und der Länge ihrer Zuleitungen abhängig. Bei der Auswahl der Filterbauteile sollte deshalb darauf geachtet werden, dass die Eigenresonanzfrequenz am oberen Ende des Frequenzbereichs liegt, in dem die Funkstörspannung maximal ist beziehungsweise in dem der Filter wirken soll.
Maßgebend für die Reduzierung der Gegentaktstörung ist die Filterspule, weil sie dem schnellen Stromanstieg und Stromabfall im Eingangskreis entgegenwirkt. Je größer die Induktivität ist, desto kleiner ist die Eigenresonanzfrequenz. Empfehlenswert ist es deshalb eine Spule mit einer Induktivität zu wählen, deren Zahlenwert kleiner ist als der der Kapazität des Filterkondensators. In der Praxis wird eine Filterinduktivität mit einem maximalen Wert von 10 µH gewählt, weil deren Eigenresonanzfrequenz je nach Bauform bei circa 30 MHz liegt.
Eine Überschreitung des zulässigen Nennstromes der Filterspule kann zur Beschädigung der Drahtwicklung führen. Anhand des Wirkungsgrads des Schaltreglers kann der effektive Eingangsstrom des Leistungsmoduls mittels der Gleichung Iin = (Vout * Iout)/(Vin * η) berechnet werden. Als Nennstrom der Filterspule sollte sicherheitshalber ein größerer Wert gewählt werden. Als Filterkondensator kann ein Flüssigelektrolyt-, Polymer- oder auch ein Keramikkondensator gewählt werden. Es muss nur sichergestellt sein, dass die Filtergüte bei der Eckfrequenz ausreichend niedrig ist.
Dimensionierung der Filter
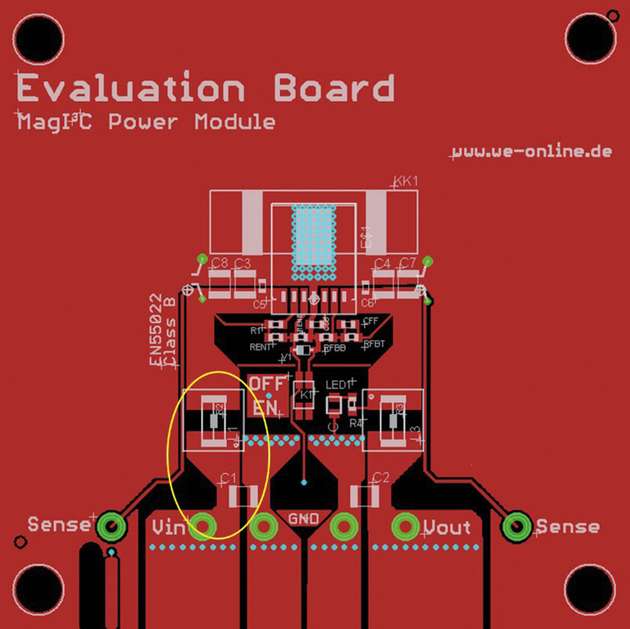
Optimalerweise sollte ein Eingangsfilter so nah wie möglich am Eingang des Power-Moduls platziert werden. Wird der Eingangsfilter aus bestimmten Gründen geometrisch weiter entfernt platziert, so kann die Leiterbahn zwischen dem Eingangsfilter und dem Power-Modul im höheren Frequenzbereich als Antenne wirken. Die zusätzliche Leiterbahninduktivität lässt sich aber auch ausnutzen, um zusammen mit einem Keramikkondensator einen zusätzlichen LC-Filter mit höherer Grenzfrequenz aufzubauen.
Moderne Power-Module, wie die MagI³C-Serie von Würth Elektronik, weisen eine vernachlässigbar kleine Restwelligkeit am Ausgang auf. Ein Ausgangsfilter ist aus diesem Grund nicht zwingend notwendig. Für den Fall, dass vom Schaltregler versorgte Komponenten über Schnittstellen, zum Beispiel Sensorschaltungen oder analoge Schaltkreise, Störsignale auskoppeln, kann aber ein Ausgangsfilter zur Filterung der Ausgangsspannung notwendig sein, um die Restwelligkeit des Power-Moduls auf ein absolutes Minimum zu reduzieren oder unerwünschte subharmonische Schwingungen zu unterdrücken.
Eingangsfilter individuell entwerfen
Anhand von einfachen Berechnungen kann ein Eingangsfilter individuell entworfen werden. Unter Berücksichtigung der Impedanzen des Filters und des Schaltreglers können Oszillationen vermieden und die Regelstabilität des Schaltreglers gewährleistet werden. Eine gezielte Auswahl der Filterkomponenten schafft eine Basis für eine optimale Auslegung des Filters. Mit einem gewissen grundlegenden Fachwissen über EMV-Prüfverfahren kann der Hardwareentwickler seine Schaltung zudem zielgerecht entwickeln und im Bedarfsfall notwendige Anpassungen des Filters selbst durchführen.







.jpg)